Question

Find the exact value and the approximate value of the perimeter of the triangle

Answer 1

the perimeter of triangle is equal to the sum of all the side of the triangle,

The perimeter of given triangle is x+y+9+3

Solve for x and y,

Apply pythagoras theorem in triangle ADC,

`\begin{gathered} AC^2=DC^2+AD^2 \\ y^2=81+AD^2^{} \\ AD^2=y^2-81 \end{gathered}`

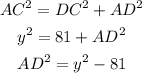
Now, in triangle ADB

Apply pythagoras,

`\begin{gathered} AB^2^{}=BD^2+AD^2 \\ x^2=9+AD^2 \\ AD^2=x^2-9 \end{gathered}`

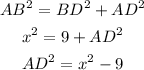
Compare the value of AD from both the equation,

`\begin{gathered} x^2-9=y^2-81 \\ x^2-y^2=-72 \end{gathered}`

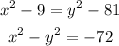
Now, in triangle ABC

`\begin{gathered} BC^2=AB^2+AC^2 \\ 12^2=x^2+y^2 \\ x^2+y^2=144 \end{gathered}`

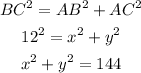
Add the equation

`\begin{gathered} x^2+x^2-y^2+y^2=-72+144 \\ 2x^2=72 \\ x^2=36 \\ x=6 \end{gathered}`

Substitute x=6 in the above equation,

`\begin{gathered} x^2_{}+y^2=144 \\ 36+y^2=144 \\ y^2=144-36 \\ y^2=108 \\ y=10.39 \end{gathered}`

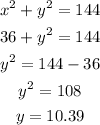
So, the value of the other side of triangle are 6, 10.39

Perimeter of triangle =sum of all sides of triangle

`\begin{gathered} \text{Perimeter}=AB+BC+AC \\ \text{Perimeter}=AB+BD+CD+AC \\ \text{Perimeter}=6+3+9+10.39_{} \\ \text{Perimeter}=28.39 \end{gathered}`

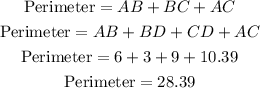
ANSWER : Perimeter is 28.39