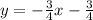Question

Consider the line y = - - X+4.4.***4.Find the equation of the line that is perpendicular to this line and passes through the point (-9, 6).Find the equation of the line that is parallel to this line and passes through the point (-9, 6).Note that the ALEKS graphing calculator may be helpful in checking your answer.Equation of perpendicular line: 0-Equation of parallel line:X0P

Answer 1

`\begin{gathered} \text{perpendicular} \\ y=(4)/(3)x+18 \\ \text{parallel} \\ y=-(3)/(4)x-(3)/(4) \end{gathered}`

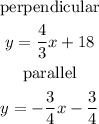
Explanation:

We have that the equation of a line in its slope and y-intercept form is the following:

`\begin{gathered} y=mx+b \\ \text{where m is the slope and b is y-intercept} \end{gathered}`

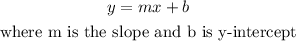
Now, when two equations are perpendicular, the slope of both are opposite, that is, the product between them is equal to -1, like this:

`\begin{gathered} m_1\cdot m_2=-1 \\ -(3)/(4)\cdot m_2=-1 \\ m_2=(4)/(3) \end{gathered}`

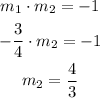
We replace the values of the point (-9, 6) and the slope to calculate the value of the y -intercept:

`\begin{gathered} 6=-9\cdot(4)/(3)+b \\ b=12+6 \\ b=18 \end{gathered}`

Therefore, the perpendicular equation that also passes through the point (-9,6) is:

`y=(4)/(3)x+18`

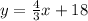
Now, when two lines are parallel, the slope is the same, therefore we calculate directly that it passes through the point (-9, 6)

`\begin{gathered} 6=-9\cdot-(3)/(4)+b_{} \\ b=6+9\cdot-(3)/(4) \\ b=-(3)/(4) \end{gathered}`

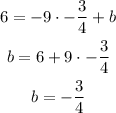
therefore, the equation of the line that is parallel to this line and passes through the point (-9, 6) is:

`y=-(3)/(4)x-(3)/(4)`