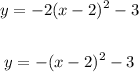Question

3. Which of the following equations would be a parabola with vertex (2,-3) that opendownwards? Select ALL.a.h.y = -2(x - 2)2 – 3i.y = (-x + 2)2 + 3C.y = -(x - 2)2 – 3b. y = -(x + 2)2 – 3y = -(x - 2)2 + 3d. y=-(x + 2)2 +3y = -(x - 2)3 +3f. y = -(x - 2)3 – 3y=-{(x - 2)2 - 3j. y = (-x - 2)2 – 3k. y = (-x + 2)2 – 3: نه1. y = (-x - 2)2 – 3m. y =} (x - 2)2 – 3g.n.y = 2(x - 2)2 - 3

Answer 1

Given:

The equation of a parabola in vertex form is given by;

`\begin{gathered} y=a(x-h)^2+k \\ \\ \text{where;} \\ (h,k)\text{ is the vertex} \\ \\ \text{Hence,} \\ h=2 \\ k=-3 \end{gathered}`

Hence, the equation of the parabola is;

Hence, from the options, the equations that have a as negative and in the form gotten above will be selected.

Therefore, the equations of a parabola with vertex (2,-3) that open downwards are;

`\begin{gathered} y=-2(x-2)^2-3 \\ \\ y=-(x-2)^2-3 \end{gathered}`