Question

Write an equation in slope - intercept form for the line that passes through the given paint andis perpendicular to the given equation.7.(-5, 2), y =1/2x-3

Answer 1

You have to find a line perpedicular to the line y=1/2x-3 that passes through the point (-5,2)

Given one line, to find another one perpedicular to it, you have to keep in mind that the slope of the perpedicular line is the negative inverse of the slope of the first one, that is:

Let the given line be:

`y_1=mx+b`

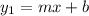
And the perpendicular line

`y_2=nx+c`

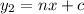
The slope of the perpendicular line will be:

`n=-(1)/(m)`

So for the line

`y=(1)/(2)x-3`

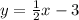
The slope is

`m=(1)/(2)`

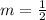
For the perpedicular line it will be:

`\begin{gathered} n=-(1)/((1)/(2))=-1\cdot(2)/(1) \\ n=-2 \end{gathered}`

Now that the slope of the perpendicular is determined, use the point slope form to find the equation of the perpedicular line:

`y-y_1=m(x-x_1)`

Replace the with m=-2 and (-5,2)

`\begin{gathered} y-2=-2(x-(-5)) \\ y-2=-2(x+5) \\ y-2=-2x-10 \\ y=-2x-10+2 \\ y=-2x-8 \end{gathered}`

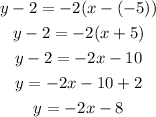
The equation perpendicular to

`y=(1)/(2)x-3`

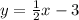
is

`y=-2x-8`

Now you can draw both lines: