We have the following prism:
• The prism has a right triangle for the base
,
• The height of the prism, h, is 8 inches (h = 8 inches)
,
• The legs of the right triangle are 4 inches, and 3 inches
And we have to determine the volume of the prism.
To find the volume of the prism we can proceed as follows:
1. We know that the general formula for calculating the volume of a prism is:

Where:
• B is the base area
,
• h is the height of the prism
2. Therefore, we need to find the base area, and we know that the base is the right triangle given above. Then the area is:
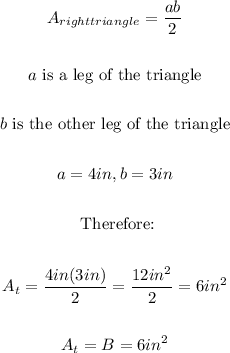
Then the base area is 6 square inches.
3. Now, we can determine the prism volume as follows:

Therefore, in summary, the prism volume is 48 cubic inches (option D.)