Answer:
a = 1
b = - 1
Step-by-step explanation:
To know the values of a and b, we need to solve the following equation:
![z=\sqrt[]{2}\lbrack\cos ((-\pi)/(4))+i\sin ((-\pi)/(4))\rbrack](https://img.qammunity.org/2023/formulas/mathematics/college/hrlfzrzlcatepaeh9v6d8u6ef1b4vekm95.png)
So, replacing cos(-π/4) by √2/2 and sin(-π/4) by -√2/2, we get:
![z=\sqrt[]{2}\cdot(\frac{\sqrt[]{2}}{2}+i\frac{-\sqrt[]{2}}{2})](https://img.qammunity.org/2023/formulas/mathematics/college/b3nucf9qukqf0zdr17cid2p5bva3f1bx1n.png)
Applying the distributive property:
![\begin{gathered} z=\frac{\sqrt[]{2}\cdot\sqrt[]{2}}{2}-\frac{\sqrt[]{2}\cdot\sqrt[]{2}}{2}i \\ z=(2)/(2)-(2)/(2)i \\ z=1-1i \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/cmjnlatvdyacqop10151qrcytsycfyl19f.png)
Therefore, we can complete the equation as:
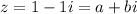
It means that a = 1 and b = - 1.