Question

I need to know the answers for 1 and 2

Answer 1

Case: Bearing and distances (Trigonometry)

Given: Position of ships A and B from the habour. The bearing of the ship B from the habour.

Ship A is 10 miles East of the habor

Ship B is south of Ship A

Ship B is at a bearing 36 degrees from the habor

Required:

To find the distance between the two ships in miles

Method:

First we sketch the problem and then apply trig ratio to solve

Considering triangle ABH and using trigonometry ratios

`\begin{gathered} \tan \theta\text{ = }(opp)/(Adj) \\ \tan 53\text{ = }(x)/(10) \\ x=\text{ 1.327 }*10 \\ x=\text{ 13.27} \end{gathered}`

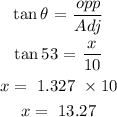
Final answer:

The two ships are 13 miles apart