2 Answers

Midhun Darvin · Answer 1 · 2022-02-12T00:21:51+0000

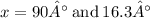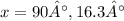
x = 90°, 16.3°

Explanation:

We are going to use the identity

$\cos x =√(1-\sin^2x)$

and substitute this into our expression so we can write

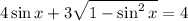
$4\sin x + 3√(1-\sin^2x) = 4$

$\Rightarrow 3√(1-\sin^2x) = 4(1 - \sin x)$

Take the square of the equation above to get

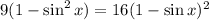
$9(1 - \sin^2x) = 16(1 - \sin x)^2$

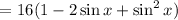
$\:\:\:\:\:= 16(1 - 2\sin x + \sin^2x)$

Rearranging the terms, we then get

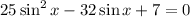
$25\sin^2x - 32\sin x + 7 = 0$

If we let
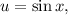$u = \sin x,$ the above equation becomes

25u^2 - 32u + 7= 0

This looks like a quadratic equation whose roots are

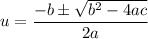
$u = (-b \pm √(b^2 - 4ac))/(2a)$

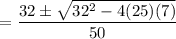
$\;\;\;\;= (32 \pm √(32^2 - 4(25)(7)))/(50)$

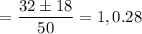
$\;\;\;\;=(32 \pm 18)/(50) = 1, 0.28$

We can then write

$\sin x = 1 \:\text{and}\;0.28$

Solving for x, we finally get

$x = 90°\:\text{and}\:16.3°$

Your comment on this question: