Question

The difference between eleven and one-fourth of a number is no less than -8

Answer 1

Inequalities

Let's call x the number.

One-fourth of the number is 1/4x

The difference between 11 and one-fourth of the number is 11 - 1/4x

That expression should be no less than -8, or equivalently it should be greater or equal to -8.

The inequality is written:

`11-(1)/(4)x\ge-8`

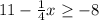
Let's solve the inequality.

First, we subtract 11:

`\begin{gathered} -(1)/(4)x\ge-8-11 \\ -(1)/(4)x\ge-19 \end{gathered}`

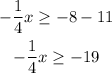
Multiply by -4. Recall that multiplying an inequality by a negative number requires to flip the sign:

`\begin{gathered} x\le-19\cdot(-4) \\ x\le76 \end{gathered}`

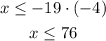
The solution can be also expressed in an interval format: (-∞,76]