ANSWER:
x =- 4
y = 3
z = 2
Explanation:
We have the following system of equations:
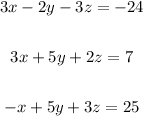
The first thing is to build the matrix from the system of equations, just like this:
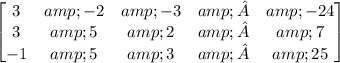
We solve by the Gauss-Jordan method, thus:
![\begin{gathered} \text{ We find the pivot in column number 1 \lparen reversing the sign in the whole row\rparen and change row number 3 to number 1} \\ \\ \begin{bmatrix}1 & -5 & -3 & ¦ & -25 \\ 3 & 5 & 2 & ¦ & 7 \\ 3 & -2 & -3 & ¦ & -24\end{bmatrix} \\ \\ \text{ We multiply row number 1 by 3} \\ \\ \begin{bmatrix}3 & -15 & -9 & ¦ & -75 \\ 3 & 5 & 2 & ¦ & 7 \\ 3 & -2 & -3 & ¦ & -24\end{bmatrix} \\ \\ \text{ We subtract row number 1 by row number 2} \\ \\ \begin{bmatrix}3 & -15 & -9 & ¦ & -75 \\ 0 & 20 & 11 & ¦ & 82 \\ 3 & -2 & -3 & ¦ & -24\end{bmatrix} \\ \\ \text{ We subtract row number 1 from row number 3 and restore it} \\ \\ \begin{bmatrix}1 & -5 & -3 & ¦ & -25 \\ 0 & 20 & 11 & ¦ & 82 \\ 0 & 13 & 6 & ¦ & 51\end{bmatrix} \\ \\ \text{ We find the pivot in column number 2 by dividing row number 2 by 20} \\ \\ \begin{bmatrix}1 & -5 & -3 & ¦ & -25 \\ 0 & 1 & (11)/(20) & ¦ & (82)/(20) \\ 0 & 13 & 6 & ¦ & 51\end{bmatrix} \\ \\ \text{ We multiply row number 2 by -5} \\ \\ \begin{bmatrix}1 & -5 & -3 & ¦ & -25 \\ 0 & -5 & -(11)/(4) & ¦ & -(41)/(2) \\ 0 & 13 & 6 & ¦ & 51\end{bmatrix} \\ \\ \text{ We subtract row number 2 from row number 1 and restore it} \\ \\ \begin{bmatrix}1 & 0 & -(1)/(4) & ¦ & -(9)/(2) \\ 0 & 1 & (11)/(20) & ¦ & (82)/(20) \\ 0 & 13 & 6 & ¦ & 51\end{bmatrix} \\ \\ \text{ We multiply row number 2 by 13} \\ \\ \begin{bmatrix}1 & 0 & -(1)/(4) & ¦ & -(9)/(2) \\ 0 & 13 & (143)/(20) & ¦ & (533)/(10) \\ 0 & 13 & 6 & ¦ & 51\end{bmatrix} \\ \\ \text{ We subtract row number 2 from row number 3 and restore it} \\ \\ \begin{bmatrix}1 & 0 & -(1)/(4) & ¦ & -(9)/(2) \\ 0 & 1 & (11)/(20) & ¦ & (82)/(20) \\ 0 & 0 & -(23)/(20) & ¦ & -(23)/(10)\end{bmatrix} \\ \\ \text{ We find the pivot in column number 3 by dividing row number 3 by -23/20} \\ \\ \begin{bmatrix}1 & 0 & -(1)/(4) & ¦ & -(9)/(2) \\ 0 & 1 & (11)/(20) & ¦ & (82)/(20) \\ 0 & 0 & 1 & ¦ & 2\end{bmatrix} \\ \\ \text{ We multiply row number 3 by -1/4} \\ \\ \begin{bmatrix}1 & 0 & -(1)/(4) & ¦ & -(9)/(2) \\ 0 & 1 & (11)/(20) & ¦ & (82)/(20) \\ 0 & 0 & -(1)/(4) & ¦ & -(1)/(2)\end{bmatrix} \\ \\ \text{ We subtract row number 3 from row number 1 and restore it} \\ \\ \begin{bmatrix}1 & 0 & 0 & ¦ & -4 \\ 0 & 1 & (11)/(20) & ¦ & (82)/(20) \\ 0 & 0 & 1 & ¦ & 2\end{bmatrix} \\ \\ \text{ We multiply row number 3 by 11/20} \\ \\ \begin{bmatrix}1 & 0 & 0 & ¦ & -4 \\ 0 & 1 & (11)/(20) & ¦ & (82)/(20) \\ 0 & 0 & (11)/(20) & ¦ & (11)/(10)\end{bmatrix} \\ \\ \text{ We subtract row number 3 from row number 2 and restore it} \\ \\ \begin{bmatrix}1 & 0 & 0 & ¦ & -4 \\ 0 & 1 & 0 & ¦ & 3 \\ 0 & 0 & 1 & ¦ & 2\end{bmatrix} \\ \\ \text{ Therefore:} \\ \\ x=-4 \\ \\ y=3 \\ \\ z=2 \end{gathered}]()
Therefore, the solution of the system is x =- 4, y = 3 and z = 2