we have
sec(θ)=5 and tan(θ) > 0
that means
The angle θ lies on the I quadrant
step 1
Find out the value of cosθ
Remember that
secθ=1/cosθ
5=1/cosθ
cosθ=1/5
step 2
Find out the value of sinθ
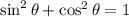
substitute the value of the cosine
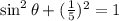
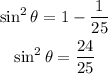
![\sin ^{}\theta=\pm\frac{2\sqrt[]{6}}{5}](https://img.qammunity.org/2023/formulas/mathematics/college/5ohuaaau8qjzfp8a3uet8aheehc8mapq01.png)
Remember that the angle lies on the first quadrant
so
the value of the sine is positive
therefore
![\sin ^{}\theta=\frac{2\sqrt[]{6}}{5}](https://img.qammunity.org/2023/formulas/mathematics/college/w0ys1i94p0e43b4n3o9ms2p0c8vgzk0b9y.png)
step 3
Find out the value of the tanθ
tanθ=sinθ/cosθ
substitute given values
![\tan \theta=\frac{\frac{2\sqrt[]{6}}{5}}{(1)/(5)}=2\sqrt[]{6}](https://img.qammunity.org/2023/formulas/mathematics/college/peopohsixna9k20brxoudgqv1dzaotn91q.png)
step 4
Find out the value of cotθ
cotθ=1/tanθ
substitute the value of tanθ
![\cot \theta=\frac{1}{2\sqrt[]{6}}](https://img.qammunity.org/2023/formulas/mathematics/college/6g7k2apajomzpe6dy2b82vfbzjposnm2mn.png)
simplify
![\cot \theta=\frac{1}{2\sqrt[]{6}}\cdot\frac{\sqrt[]{6}}{\sqrt[]{6}}=\frac{\sqrt[]{6}}{12}](https://img.qammunity.org/2023/formulas/mathematics/college/hdnx967tybhx6sltlznpdoxi3zs4m7ddfe.png)
step 5
Find out the value of cscθ
cscθ=1/sinθ
substitute the value of the sine
![\csc \theta=\frac{1}{\frac{2\sqrt[]{6}}{5}}=\frac{5}{2\sqrt[]{6}}](https://img.qammunity.org/2023/formulas/mathematics/college/qjyg0btt84plrgbqxlt2hv2l5ohpxjvggy.png)
simplify
![\csc \theta=\frac{5}{2\sqrt[]{6}}\cdot\frac{\sqrt[]{6}}{\sqrt[]{6}}=\frac{5\sqrt[]{6}}{12}](https://img.qammunity.org/2023/formulas/mathematics/college/1kje43uf8xt9np8jo42ukeuqxs29sttvh2.png)