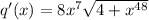We are given the definite integral:
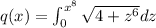
We need to find q'(x).
We can use the fundamental theorem of calculus to solve this. Given a function F(x):
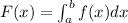
Then:
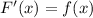
Thus, we can find the antiderivative q'(x), using the fundamental theorem of calculus and the chain rule:
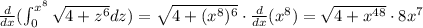
The answer is: