Answer:
![\begin{gathered} p(\sqrt[]{2})=12\sqrt[]{2}-9 \\ p(-(1)/(2))=2.5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/lof3jkhq22haslbbk0ehh7j2hh118wqmpc.png)
Explanations:
Given the polynomial function
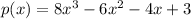
We are to find the equivalent value when x = √2 and x = -1/2
a) Substitute x = √2 into the polynomial function to have:
![\begin{gathered} p(\sqrt[]{2})=8(\sqrt[]{2})^3-6(\sqrt[]{2})^2-4(\sqrt[]{2})+3 \\ p(\sqrt[]{2})=8\lbrack(\sqrt[]{2})^2\cdot\sqrt[]{2}\rbrack-6(2)-4\sqrt[]{2}+3 \\ p(\sqrt[]{2})=8(2\sqrt[]{2})-12-4\sqrt[]{2}+3 \\ p(\sqrt[]{2})=16\sqrt[]{2}-4\sqrt[]{2}-12+3 \\ p(\sqrt[]{2})=12\sqrt[]{2}-9 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/6j55jbfr4pjdix3q9exeap2jje0p08bvpa.png)
b) Substitute x = -1/2 into the polynomial function to have:
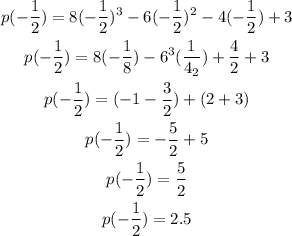
Therefore the value of the polynomial when x = -1/2 is 2.5