Question

Use the rational zeroes theorem to factor the function f(x) = x3 – 21x + 20 completely.(A) (x - 1)(x + 4)(x + 5)(B) (x + 1)(x - 4)(x + 5)(C) (x - 1)(x – 4)(x - 5)(D) (x - 1)(x – 4)(x + 5)(E) (x + 1)(x - 4)(x - 5)

Answer 1

f(x) = x³ - 21x + 20

factors of 20 (the independent term): 1, 2, 4, 5, 10, 20

factors of 1 (the leading coefficient): 1

Using the rational zeroes theorem, the possible zeros of f(x) are:

`\pm(1,2,4,5,10,20)/(1)=\pm1,\pm2,\pm4,\pm5,\pm10,\pm20`

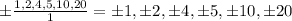
Substituting x = -5 into f(x), we get:

f(-5) = (-5)³ - 21(-5) + 20

f(-5) = -125 + 105 + 20

f(-5) = 0

Substituting x = 1 into f(x), we get:

f(1) = 1³ - 21(1) + 20

f(1) = 1 - 21 + 20

f(1) = 0

Substituting x = 4 into f(x), we get:

f(4) = 4³ - 21(4) + 20

f(4) = 64 - 84 + 20

f(4) = 0

Therefore,

f(x) = x³ - 21x + 20 = (x - 1)(x - 4)(x + 5)