From the question,
The probability of picking a pink marble is
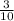
If the marbles are picked with replacement
This implies that the probability of picking a pink marble will remain

If 100 there is 100 draw
Then the expected number of times the pink marble will be picked is
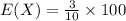
Simplify the equation

Therefore, the expected number of time the pink marble will be picked is 30