Question

I need help with my homework PLEASE CHECK WHEN FINISHED

Answer 1

The recursive formula is given below as

`\begin{gathered} a_1=7 \\ a_n=-3+a_((n-1)) \end{gathered}`

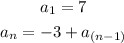
Step 1:

To figure out the value of the forurth term, we will substitute the value of

`n=4`

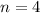
By substituting the n=4, we will have

`\begin{gathered} a_(n)=-3+a_((n-1)) \\ a_4=-3+a_((4-1)) \\ a_4=-3+a_3 \end{gathered}`

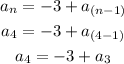
Step 2:

Calculate the second term and the third term

`\begin{gathered} a_(n)=-3+a_((n-1)) \\ a_2=-3+a_((2-1)) \\ a_2=-3+a_1 \\ a_2=-3+7 \\ a_2=4 \\ \\ a_(n)=-3+a_((n-1)) \\ a_3=-3+a_((3-1)) \\ a_3=-3+a_2 \\ a_3=-3+4 \\ a_3=1 \end{gathered}`

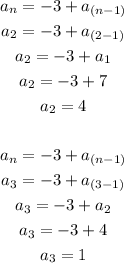
Step 3:

Substitute the value of the third term in the equation below

`\begin{gathered} a_(4)=-3+a_(3) \\ a_4=-3+1 \\ a_4=-2 \end{gathered}`

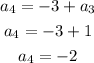
Hence,

The final answer is

`\Rightarrow-2`

OPTION C is the right answer