Answer:
227/210
Step-by-step explanation:
First, we need to find the least common multiple between 21 and 10, so:
multiples of 21: 21, 42, 63, 84, 105, 126, 147, 168, 189, 210,...
multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120, 130, 140, 150, 160, 170, 180, 190, 200, 210,...
Therefore, the minimum multiple is 210.
Now, to add the fractions, we need to rewrite the fractions as follows:
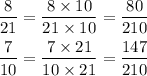
Finally, we can add the numerators of the fractions to get:
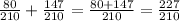
Therefore, the answer is 227/210