Question

An air-filled pipe is found to have successive harmonics at 800 Hz , 1120 Hz , and 1440 Hz . It is unknown whether harmonics below 800 Hz and above 1440 Hz exist in the pipe. What is the length of the pipe?

Answer 1

Answer:

The length of the pipe = 53.59 cm

Step-by-step explanation:

The given successive harmonics are:

800 Hz, 1120 Hz, and 1440 Hz

The difference between two successive harmonics is 2 times the fundamental frequency

That is:

`\begin{gathered} 2f_o=1120-800 \\ 2f_o=320 \\ f_0=(320)/(2) \\ f_o=160Hz \end{gathered}`

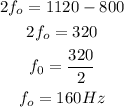
The fundamental frequency for closed pipes is given by the formula:

`f_o=(v)/(4L)`

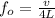
where v is the speed of sound, and is given as v = 343 m/s

Substitute v = 343 and f₀ = 160 into the formula

`\begin{gathered} 160=(343)/(4L) \\ L=(343)/(4(160)) \\ L=0.5359m \\ L=0.5359*100cm \\ L=53.59\text{ cm} \end{gathered}`

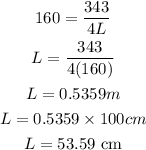
The length of the pipe = 53.59 cm