To solve this, it is necessary to use a system of equations
Take x as the number of bags of candy and y as the number of bags of cookies.
You know that there were 6 more bags of cookies than candy sold it means:
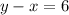
You also know that the sales equaled $46.00 and the unit cost of each product, the equation that represents the sales is:

Solve the system of equations:
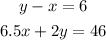
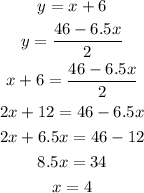
Using this value of x, find the value of y:
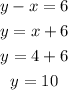
The solution is x=4 and y=10, which means that there were sold 4 bags of candy and 10 bags of cookies