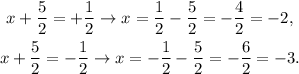Step-by-step explanation
We must solve the following quadratic equation by completing squares:
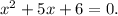
1) First, we rewrite the equation in the following way:
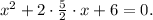
2) We sum to both sides of the equation (5/2)², get:
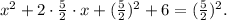
3) Expressing the first term as a square, we have:
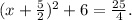
4) Passing the +6 at the left as -6 at the right:
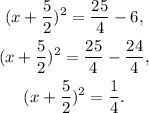
5) By taking the square root on both sides, we get two solutions:
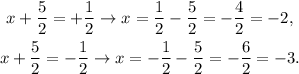
Answer
1) Re-writing the equation:
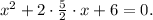
2) Summing (5/2)² on both sides:
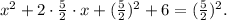
3) Expressing the first term as a square:
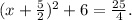
4) Simplifying:
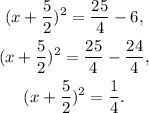
5) Taking the square root: