We want to find the following probability:
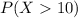
where X is a normal random variable with mean 13.3 and standard deviation 1.1. To find this probability let's normalize the random variable; to do this we use the z-score given by:

Then, in this case, we have:
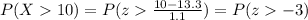
Using the standard normal table, we have:
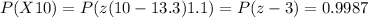
Therefore, the probability of purchasing an item with a lifespan greater than 10 years is 0.9987