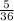Step 1: Let us find the possible scenario that when the coin is tossed twice, the first toss plus the second toss would give us a sum of 8.
From the tree diagram:
If a first toss gives 1, there's no other possibility of getting a second toss that would give us a sum of 8. The highest possible value the teacher can get on the second toss is 6.
The highest possible sum is 1 + 6 = 7.
So we cannot get a sum of 8, if the teacher records a face value of 1 in the first toss.
If the teacher records 2 in the first toss, the teacher can get a sum of 8 if he tosses the coin and gets a 6 on the second toss.
2+6 = 8
(This is the first possible case for a sum of 8)
If the teacher records 3 in the first toss, the teacher can get a sum of 8 if he tosses the coin and gets a 5 on the second toss.
3+5 = 8
(This is the second possible case for a sum of 8)
If the teacher records 4 in the first toss, the teacher can get a sum of 8 if he tosses the coin and gets a 4 on the second toss.
4+4 = 8
(This is the third possible case for a sum of 8)
If the teacher records 5 in the first toss, the teacher can get a sum of 8 if he tosses the coin and gets a 3 on the second toss.
5+3 = 8
(This is the fourth possible case for a sum of 8)
If the teacher records 6 in the first toss, the teacher can get a sum of 8 if he tosses the coin and gets a 2 on the second toss.
6+2 = 8
(This is the fifth possible case for a sum of 8)
Number of cases for a sum of 8 = 5
The total possible sum of tossing a coin twice = 36
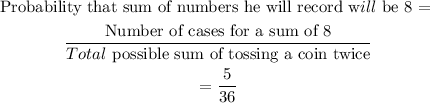
The final answer is