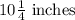Question

I need help understanding how to find the dimension of a geometric figures.I need help understand how to find the value of the hypotenuse

Answer 1

We want to obtain the length of the hypotenuse.

But we must obtain x first.

Since this is a right-angle triangle, we must employ Pythagoras Theorem;

`(x+10)^2=10^2+(9x)^2`

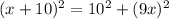
The square of the hypotenuse is equal to the sum of the square of the other two sides, let's expand the equation, we obtain;

`\begin{gathered} x^2+20x+100=100+81x^2 \\ \text{collect like terms to obtain} \\ 81x^2-x^2-20x+100-100=0 \\ 80x^2-20x=0 \\ 80x^2=20x \\ \text{divide both sides by 20x} \\ 4x=1 \\ x=(1)/(4)\text{ } \end{gathered}`

Thus, the length of the hypotenuse is

`10(1)/(4)\text{ inches}`