Question

-4x -8 < -24 OR -5x < 40

Answer 1

Given the expressions:

`\begin{gathered} -4x-8<-24 \\ or \\ -5x<40 \end{gathered}`

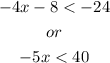
To find the solution set, we have to solve both inequalities at the same time and take the union of both cases:

`\begin{gathered} first\text{ case:} \\ -4x-8<-24 \\ \Rightarrow-4x<-24+8=-16 \\ \Rightarrow x>-(16)/(-4)=4 \\ x>4 \\ \text{second case:} \\ -5x<40 \\ \Rightarrow x>(40)/(-5)=-8 \\ x>-8 \end{gathered}`

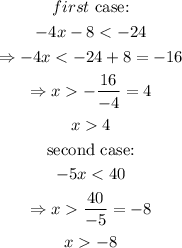
in the first case we have that x>4 and in the second case x>-8. Since the inteval (4,oo) is contained in the interval (-8,oo), we have the following:

therefore, the solution set is (-8,oo)