Question

a circular sector has a radius r= 5.3 and a central angle theta= 140°. determine the arc length and the area.

Answer 1

Step-by-step explanation:

First we must know what data the exercise gives us and thus replace them correctly in the two formulas; in the formula for the area of ​​the arc and in the formula to find the length.The data is as follows:

-Radius(r)=5.3

-angle theta(θ)=140 degrees.

To find the area of ​​the circular sector in degrees we must use the following formula:

`\begin{gathered} \text{Area:}=(\pi* R^2*\emptyset)/(360) \\ \text{Area}=(\pi*(5.3)^2*(140))/(360) \\ \text{Area}=(\pi*28.09*140)/(360) \\ \text{Area}=(12.534.627)/(360) \\ \text{Area}=34,818 \\ \text{ANSWER:Area is 34.18} \end{gathered}`

To find the length of the arc we must use the following formula:

`\begin{gathered} L=(2*\pi* R*\emptyset)/(360) \\ L=(2*\pi*5.3*140)/(360) \\ L=(2*\pi*742)/(360) \\ L=(4,662.12)/(360) \\ L=12.95 \\ \text{ANSWER: The length is 12.95} \end{gathered}`

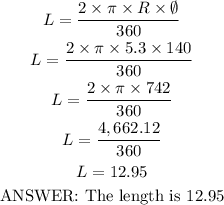
IMPORTANT NOTE:

The formulas that were used to find the longitude and area of ​​the arc were in degrees since the exercise indicated that the angle theta is in degrees