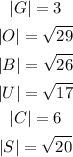Question

Graph abs label each complex number on the given plane

Answer 1

Given:

There are given that complex numbers:

`\begin{gathered} G=3i \\ O=2+5i \\ B=5-i \\ U=-1-4i \\ C=-6 \\ S=-4+2i \end{gathered}`

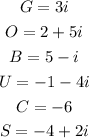
Step-by-step explanation:

According to the question:

We need to find the absolute value of the all above given complex numbers:

So,

To find the absolute value of the complex number, we need to use the properties of the complex number:

So,

From the properties of the complex numbers:

`|a+ib|=√(a^2+b^2)`

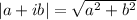
So,

From the first complex number:

`\begin{gathered} G=3\imaginaryI \\ |G|=√(0^2+3^2) \\ |G|=√(9) \\ |G|=3 \end{gathered}`

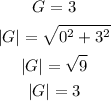
From the second complex number:

`\begin{gathered} O=2+5\imaginaryI \\ |O|=√(2^2+5^2) \\ |O|=√(4+25) \\ |O|=√(29) \end{gathered}`

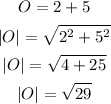
From the third complex number:

`\begin{gathered} B=5-\imaginaryI \\ |B|=√(5^2+(-1)^2) \\ |B|=√(25+1) \\ |B|=√(26) \end{gathered}`

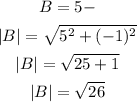
From the fourth complex number:

`\begin{gathered} U=-1-4\imaginaryI \\ |U|=√((-1)^2+(-4)^2) \\ |U|=√(1+16) \\ |U|=√(17) \end{gathered}`

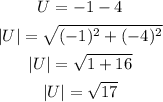
From the fifth complex number:

`\begin{gathered} C=-6 \\ |C|=√((-6)^2+0^2) \\ |C|=√(36) \\ |C|=6 \end{gathered}`

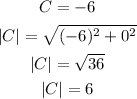
Then,

From the sixth complex number:

`\begin{gathered} S=-4+2\imaginaryI \\ |S|=√((-4)^2+(2)^2) \\ |S|=√(16+4) \\ |S|=√(20) \end{gathered}`

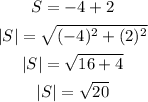
Final answer:

Hence, the absolute of the given complex number is shown below:

`\begin{gathered} \lvert G\rvert=3 \\ \lvert O\rvert=√(29) \\ \lvert B\rvert=√(26) \\ \lvert U\rvert=√(17) \\ \lvert C\rvert=6 \\ \lvert S\rvert=√(20) \end{gathered}`