Let's begin by listing out the information given to us:
a.
Henry:
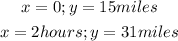
Tasha:

As such, Tasha's balloon was farther from the town at the start than Henry's balloon (it was farther by 10 miles)
b.
After 2 hours, their balloon had travelled this far:
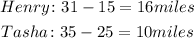
Therefore, Henry's balloon travelled faster than Tasha's balloon