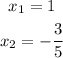Question

Solve the quadratic by factoring.5x2 – 10 = 2x – 7

Answer 1

Given the followin Quadratic equation:

`5x^2-10=2x-7`

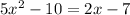
You need to follow these steps in order to solve it by factoring:

1- Subtract 2x from both sides of the equation:

`\begin{gathered} 5x^2-10-(2x)=2x-7-(2x) \\ 5x^2-10-2x=-7 \end{gathered}`

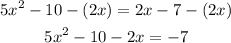
2. Add 7 to both sides of the equation:

`\begin{gathered} 5x^2-10-2x+(7)=-7+(7) \\ 5x^2-2x-3=0 \end{gathered}`

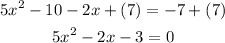
Now the equation has this form:

`ax^2+bx+c=0`

3. You can notice that the leading coefficient is:

`a=5`

Then, multiply and divide the trinomial by 5:

`\begin{gathered} (5(5x^2-2x-3))/(5)=0 \\ \\ ((5x)^2-2(5x)-3(5))/(5)=0 \\ \\ ((5x)^2-2(5x)-15)/(5)=0 \end{gathered}`

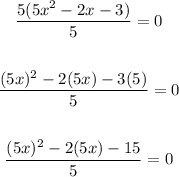
4. Now let's factor it:

Find two numbers whose sum is -2 and whose product is -15. These would be 3 and -5. Then:

`((5x-5)(5x+3))/(5)=0`

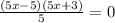
5. Simplify and find the solutions:

`\begin{gathered} ((5x-5)(5x+3))/(5)=0 \\ \\ (x-1)(5x+3)=0 \\ \\ x_1=1 \\ \\ x_2=-(3)/(5) \end{gathered}`

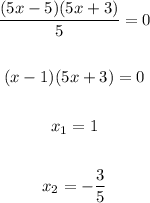
The answer is:

`\begin{gathered} x_1=1 \\ x_2=-(3)/(5) \end{gathered}`