Question

You invest $20,000 into an account that pays 4.5% compounding quarterly. How much interest did you earn after 6 years?

Answer 1

To find how much interest is earned after 6 years, we apply the following formula:

`\text{Interest}=P(1+(r)/(100n))^(tn)-P`

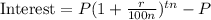
where:

- P = amount initially invested = $20,000

- r = percentage rate at which the amount was invested = 4.5

- t = the duration for which the investment was made = 6 years

- n = the frequency at which the interest is compounded = quarterly = 4

Now, we simply substitute the values into the formula to obtain the Interest, as follows:

`\begin{gathered} \text{Interest}=P(1+(r)/(100n))^(tn)-P \\ \Rightarrow\text{Interest}=20000(1+(4.5)/(100(4)))^(6*4)-20000 \\ \Rightarrow\text{Interest}=20000(1+(4.5)/(400))^(24)-20000 \\ \Rightarrow\text{Interest}=20000(1+0.01125)^(24)-20000 \end{gathered}`
`\Rightarrow\text{Interest}=20000(1.01125)^(24)-20000`
`\begin{gathered} \Rightarrow\text{Interest}=20000*1.3080-20000 \\ \Rightarrow\text{Interest}=26160-20000 \\ \Rightarrow\text{Interest}=6160\text{ dollars} \end{gathered}`

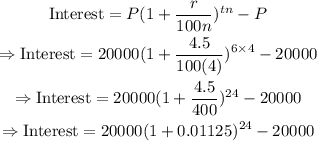
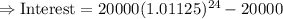
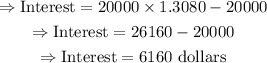
Therefore, the interest earned after 6 years is: $6,160