Question

3. Two lenses with focal length 2 m are placed 4 m apart. An object is placed 1 m in front of the first lens. Where will its image appear relative to the second lens?1. -0.5 m2. 2/3 m3. -2 m4. 3 m

Answer 1

Given:

D1 = 2 m

D2 = 4 m

Distance between object and lens = 1 m

Let's find where the image will appear relative to the second lens.

To find the distance, apply the formula:

`(1)/(v)-(1)/(u)=(1)/(f)`

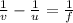
Thus, we have:

`\begin{gathered} (1)/(1)+(1)/(u)=(1)/(2) \\ \\ (1)/(u)=(1)/(2)-(1)/(1) \\ \\ (1)/(u)=-(1)/(2) \\ \\ u=-2\text{ m} \end{gathered}`

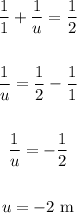
Now, we have the equation:

`\begin{gathered} v_2=L-f \\ \\ v_2=4--2 \\ \\ v_2=4+2 \\ v_2=6\text{ m} \\ \end{gathered}`

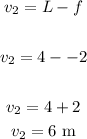
Now, let's use the Lens equation:

`\begin{gathered} (1)/(6)+(1)/(u_2)=(1)/(2) \\ \\ (1)/(u_2)=(1)/(2)-(1)/(6) \\ \\ (1)/(u_2)=(3-1)/(6)=(2)/(6) \\ \\ u_2=(6)/(2) \\ \\ u_2=3\text{ m} \end{gathered}`

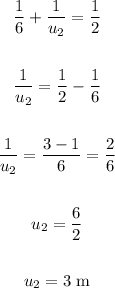
Now, to find the image distance relative to the second lens, we have:

`-(u_2)/(v_2)=-\frac{3\text{ m}}{6\text{ m}}=-0.5\text{ m}`

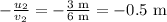
Therefore, the image will appear -0.5 m relative to the second lens.

ANSWER:

1.) -0.5 m