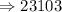.
Answer:
The function is given below as
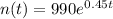
The exponential function is given below as
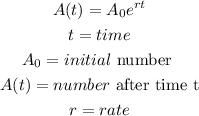
By comparing coefficients, we will have
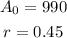
Hence,
the rate will be
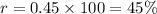
Therefore,
The rate is
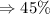
Step 2:
To figure out the initial population, we will substitute t=0 in the function above
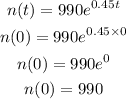
Hence,
The initial population of the culture is
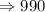
Step 3:
To figure out the number of bacteria at t=7, we will have
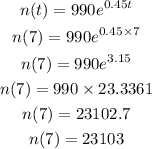
Hence,
The number of bacteria at time t=7 will be