Given:
• Initial velocity = 19 m/s
,
• Acceleration = 4.1 m/s²
Let's find how long it will take before its final velocity is equal to three times its initial velocity.
Apply the motion formula:
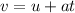
Where:
v is the final velocity
u is the initial velocity
a is the acceleration
t is the time.
Since we are to find the time it will take the final velocity to equal 3 times the initial velocity, we have:
v = 3u
Substitute 3u for v in the equation.
We have:
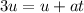
Substitute values into the formula and solve for t:
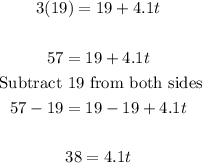
Divide both sides by 4.1:
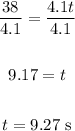
Therefore, it will take 9.27 seconds before its final velocity is equal to three times its initial velocity.
ANSWER:
9.27 s