Question

The product of two consecutive even integers is 224. find the integers

Answer 1

• 14 and 16

,

• -16 and -14.

Step-by-step explanation:

Let the smaller of the two consecutive even integers = x

The larger of the two consecutive even integers = x+2

We are told that their product is 224, therefore:

`\begin{gathered} x(x+2)=224 \\ x^2+2x=224 \end{gathered}`

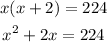
We solve the resulting quadratic equation for x.

`\begin{gathered} x^2+2x-224=0 \\ x^2+16x-14x-224=0 \\ x(x+16)-14(x+16)=0 \\ (x-14)(x+16)=0 \\ x-14=0\text{ or }x+16=0 \\ x=14\text{ or x=-16} \end{gathered}`

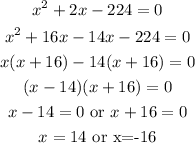
Therefore, the two consecutive even integers are:

• 14 and 16

,

• -16 and -14.

,

•