Question

How do I find the value of x and y?

Answer 1

It is important to remember that the total arc length measure of the entire circle is 360°.

In the figure that we have, what comprises the entire circle are the following arcs with their corresponding arc length:

1. AB = ??

2. BC = 152°

3. CD = 80°

4. DA = 84°

Subtracting the given arc lengths from 360, we get the measure of arc AB.

`360-152-80-84=44`

The arc length of arc AB is 44°.

Now, in the figure, the inscribed angle BCD intercepts the arcs DA and AB which the total measure of its arc length is 84° + 44° =128°.

Another important note to remember is that the measure of the inscribed angle is half the measure of the intercepted arc.

Hence, the inscribed angle BCD is half the measure of the intercepted arc length 128°. The measure of inscribed angle BCD is 64°. Since inscribed angle BCD is 4x, then we can say that:

`\begin{gathered} \angle BCD=4x \\ 64=4x \\ \text{Divide 4 both sides.} \\ 16=x \end{gathered}`

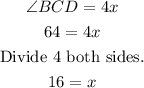
The value of x is 16.

To solve for y, we have the inscribed angle ADC = 7y intercepting the arcs AB and BC in which the total measure of its arc length is 44 + 152 = 196°.

Apply the note mentioned above, we can say that the measure of the inscribed angle ADC is 98°, that is half the arc length 196°.

Since angle ADC = 7y, we can say that 7y = 98.

`\begin{gathered} \angle ADC=7y \\ 98=7y \\ \text{Divide both sides by 7.} \\ 14=y \end{gathered}`

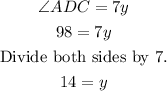
The value of y is 14.