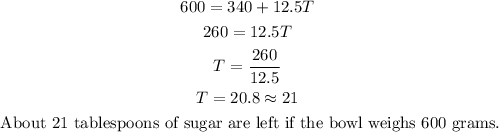Question

2a. Write an equation to represent the relationship between the totalweight of the bowl in grams, W. and the tablespoons of sugar, T.*Your answer2b. When the sugar bowl is full, it weighs 740 grams. How manytablespoons of sugar can the bowl hold? Show your reasoning. *Your answer2c. The graph represents the relationship between the number oftablespoons of sugar in the bowl and the total weight of the bowl. Whichpoint on the graph could represent your answer to the previous question?

Answer 1

`\begin{gathered} 2a\text{. }W(T)=340+12.5T \\ 2b\text{. The bowl can hold 32 tablespoons of sugar.} \\ 2c\text{. 32 tablespoons of sugar represent point D on the graph.} \\ 2d\text{. About 21 tablespoons of sugar are left if the bowl weighs 600 grams.} \end{gathered}`

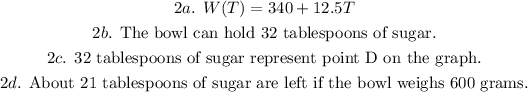
Explanation:

This situation can be represented by a linear function since it has an initial value and it changes by a constant rate of change.

Linear functions are given as:

Let x be the number of tablespoons of sugar

2a.

`\begin{gathered} W(T)=\text{initial weight+}(\text{rate of change)(tablespoons}) \\ W(T)=340+12.5T \end{gathered}`

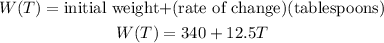
2b. If the sugar bowl weighs 740 grams when it is full, then to determine the number of tablespoons of sugar, substitute W(T)=740 and solve for T.

`\begin{gathered} 740=340+12.5T \\ 12.5T=740-340 \\ 12.5T=400 \\ T=(400)/(12.5) \\ T=32\text{ } \\ \text{ The bowl can hold 32 tablespoons of sugar.} \end{gathered}`

2c. By looking at the graph, we can see that at the x-axis, 32 tablespoons represent point D

2d. Now, to determine how many tablespoons are left if the weight is 600 grams. Substitute W(T)=600 as in point 2b.

`\begin{gathered} 600=340+12.5T \\ 260=12.5T \\ T=(260)/(12.5) \\ T=20.8\approx21 \\ \text{ About 21 tablespoons of sugar are left if the bowl weighs 600 grams.} \end{gathered}`