Given :
the function is,
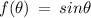
in the range,
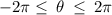
to find :
graph the function.
Step-by-step explanation:
a normal sin graph will look like the graph below,
here the graph, the graph has the interval,
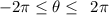
thus, the end point of the graph will be,
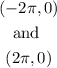
Final answer:
the graph will is as follows,