PART A
To find the solutions to the system, we can multiply the second equation by -2

Then, we combine the equations and solve for y
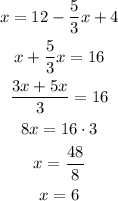
Now, we find y using x-value
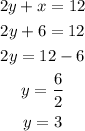
Hence, the ordered pair where the graphs intersect is (6,3).
Part B.
To verify that the point (6,3) is a solution of 2y+x = 12, we just have to replace it
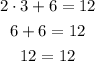
As you can observe, it satisfies the equation, so it's a solution to it.
Part C.
To verify that the point (6,3) is a solution of the second equation, we just have to replace it
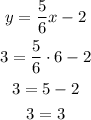
Hence, the point is a solution to the second equation too.
PART D.
Point (4,4) couldn't be a solution of the system because it has a unique solution, which is (6,3). Additionally, the point (4,4) only satisfies the first equation but not the second one, and the solution must be a solution to both equations.