Question

The functions f(x), g(x), and h(x) are shown below. Select the option that represents the ordering of the functions according to their average rates of change on the interval −3≤x≤−2 goes from least to greatest.

Answer 1

The average rate of change of a function f in an interval (a,b) is given by:

`m=(f(b)-f(a))/(b-a)`

From the graph on function f we notice that f(-3)=-5 and f(-2)=-10, then forf we have:

`\begin{gathered} m_f=(f(-2)-f(-3))/(-2-(-3)) \\ m_f=(-10-(-5))/(3-2) \\ m_f=(-10+5)/(1) \\ m_f=-5 \end{gathered}`

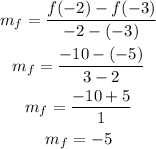
Fro the table defining dfunction g we have that g(-3)=19 and g(-2)=12, then we have:

`\begin{gathered} m_g=(g(-2)-g(-3))/(-2-(-3)) \\ m_g=(12-19)/(1) \\ m_g=-7 \end{gathered}`

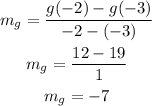
Finally, for function h we have:

`\begin{gathered} m_h=(g(-2)-g(-3))/(-2-(-3)) \\ m_h=(\lbrack-(-2)^2+(-2)+2\rbrack-\lbrack-(-3)^2+(-3)+2\rbrack)/(-2-(-3)) \\ m_h=((-4-2+2)-(-9-3+2))/(1) \\ m_h=((-4)-(-10))/(1) \\ m_h=(-4+10)/(1) \\ m_h=6 \end{gathered}`

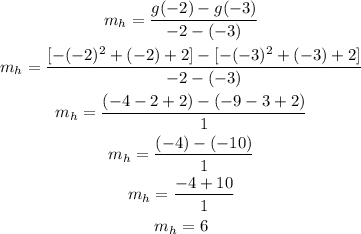
Now, that we have all the average rate of change we notice that:

[tex]m_gTherefore, the order we have is g(x), f(x), h(x)