Question

EY is the median of triangle RET, RY=2z-1, and TY=4z-11. Find RT. RT=

Answer 1

Given the triangle RET

The median of the triangle EY, joins the vertex E with the midpoint of the opposite line RT.

The midpoint Y divides the side RT into two equal segments RY and TY

`RY=TY`

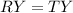
If RY=2z-1 and TY=4z-11, then

`2z-1=4z-11`

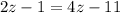
From this expression, you can calculate the value of z

First, pass the z term to the left side of the equation and the number to the right side of the equation by applying the opposite operation to both sides of the eqaution

`\begin{gathered} 2z-1=4z-11 \\ 2z-4z-1=4z-4z-11 \\ -2z-1=-11 \\ -2z-1+1=-11+1 \\ -2z=-10 \end{gathered}`

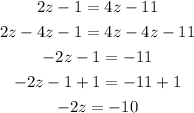
Second, divide both sides of the equation by -2 to determine the value of z

`\begin{gathered} -(2z)/(-2)=-(10)/(-2) \\ z=5 \end{gathered}`

Now that we know the value of z, you can calculate the line segment RT as:

`\begin{gathered} RT=RY+TY \\ RT=2\cdot RY \\ RT=2(2z-1) \\ RT=2(2\cdot5-1) \\ RT=18 \end{gathered}`

The length of RT is 18 units