Gabriel deposits 2500 into two accounts i and ii, for 3 years. Account i has a 4% simple interest rate and account ii has a 4% compound interest (annually)
To determine the sum of both accounts' balances after a 3-year time period, the first step is to calculate how much will the Accrued amount be for both accounts.
Account i:
To determine the accrued amount for an account with the simple interest you have to use the following formula:
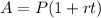
Where
A is the accrued amount after t time intervals
P is the principal amount
r is the interest rate (expressed as a decimal value)
t is the time interval (measured in years)
The principal amount is P=2500
The interest rate expressed as a decimal value:
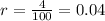
The time period is t=3 years.
Replace the information on the formula to calculate the accrued amount for account i:
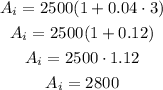
After 3 years the balance for account i will be Ai=$2800
Account ii
To calculate the accrued amount for an account that compounds annually you have to use the following formula:
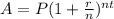
Where
A is the accrued amount
P is the principal amount
r is the interest rate expressed as a percentage
n is the number of compound periods per unit of time
t is the time periods measured in years
For this account:
P=2500
r=4/100=0.04
n=1 → the account compounds annually, which means that there is one compound period per year
t=3 years
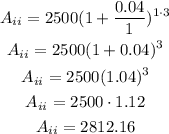
After 3 years the balance for account ii will be Aii=$2812.16
Now what's left is to add both amounts to determine the final balance between both accounts:
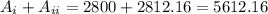
The final balance will be $5612.16