Answer:
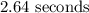
Step-by-step explanation:
Here, we want to calculate the number of minutes it takes the ball to hit the ground
To calculate this, we have to solve the quadratic equation and record the positive t value (this is because time t, cannot be negative)
Mathematically, we have the equation to use as follows:
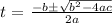
where a is the coefficient of t^2 which is -16
b is the coefficient of t which is -15
c is the last number which is 151
Substituting the values, we have it that:
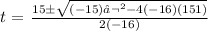
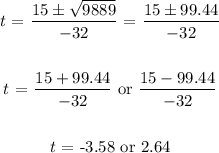
Since t cannot be negative, we have t as 2.64 seconds