Question

the ratio of the measure of three angles of a triangle is 10:8:6. Find the measure of the smallest angle

Answer 1

There are, at least, two ways to answer this question. One way is as follows:

1. We have that the ratio of the three angles is 10:8:6.

2. We know that the three inner angles of a triangle sum up to 180 degrees.

Then, we can express the problem as follows:

`10x+8x+6x=180`

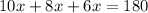
And now, we need to add the coefficients of the like terms:

`(10+8+6)x=180\Rightarrow24x=180`

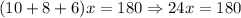
Dividing both sides of the equation by 24, we have:

`(24)/(24)x=(180)/(24)\Rightarrow x=(15)/(2)=7.5`

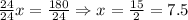
Then, we this value for x, we can determine the value for each of the angles of the triangle:

The largest angle:

`10\cdot(15)/(2)=5\cdot15=75\Rightarrow m\angle L=75`

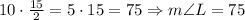
The medium size angle:

`8\cdot(15)/(2)=4\cdot15=60\Rightarrow m\angle M=60`

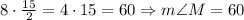
And, finally, the smallest angle is:

`6\cdot(15)/(2)=3\cdot15\Rightarrow m\angle S=45`

If we check the angles, we have that:

75 + 60 + 45 = 180

We also can check this, if we express the question as follows:

We have that the total of the ratios is: 10 + 8 + 6 = 24. Then, the first angle is the fraction of 10/24 (10 over the total) of the 180 degrees of the sum of the inner angles of the triangle:

`(10)/(24)=(5)/(12)\Rightarrow(5)/(12)\cdot180=75`

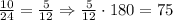
The second angle is:

`(8)/(24)=(1)/(3)\Rightarrow(1)/(3)\cdot180=60`

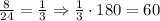
And the smallest angle is:

`(6)/(24)=(1)/(4)\Rightarrow(1)/(4)\cdot180=45`

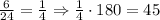
Therefore, with both methods, we have that the measure of the smallest angle is 45 degrees.

The ratio to the lowest terms is:

75:60:45 = 10:8:6 = 5:4:3