Question

17. What is the area of the square that can be drawn on side c of each triangle?

Answer 1

The area of any square is

`A=s^2`

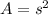
Where "s" is the length of the side of the square

a)

The given triangle has:

Hypotenuse is c

Two legs of the right angle are 21 cm and 28 cm

The area of the square of side length c is

`A=c^2`

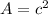
Then we will use the Pythagorean relationship to find c^2

`\begin{gathered} c^2=(21)^2+(28)^2 \\ c^2=441+784 \\ c^2=1225 \end{gathered}`

Then the area of the square of side c is 1225 square cm

b)

The given triangle has:

Hypotenuse of length 13 mm

Two legs of the right angle are 5 mm and c

The area of the square of the side length c is

`A=c^2`

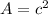
We will use the Pythagorean relationship to find it

`\begin{gathered} (13)^2=(5)^2+c^2 \\ 169=25+c^2 \end{gathered}`

Subtract 25 from both sides

`\begin{gathered} 169-25=25-25+c^2 \\ 144=c^2 \end{gathered}`

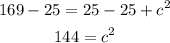
The area of the square of side length c is 144 square mm