Question

What is the slope of a line that is perpendicular to the line whose equation is 0.5x−5y=9?A. −10B. −5/9C. 1/10D. −1/10

Answer 1

To determine the slope of a line that is perpendicular to the line with equation

`0.5x-5y=9`
`\begin{gathered} 0.5x-5y=9 \\ 0.5x-9=5y \\ 5y=0.5x-9 \\ \text{divide through by 5} \\ (5y)/(5)=(0.5x)/(5)-(9)/(5) \\ y=0.1x-(9)/(5) \end{gathered}`

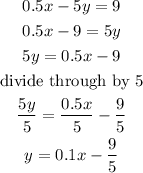
The equation of a straight line is y =mx+c

`\begin{gathered} y=mx+c \\ \text{compare with } \\ y=0.1x-(9)/(5) \\ m_1=\text{ 0.1} \end{gathered}`

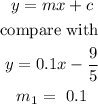
Two lines are perpendicular if m1. m2 = -1 Another way of saying this is the slopes of the two lines must be negative reciprocals of each other.

`\begin{gathered} m_1.m_2\text{ = -1} \\ 0.1m_2\text{ = -1} \\ m_2\text{ = }(-1)/(0.1) \\ m_2\text{ = -10} \end{gathered}`

Hence the slope of the line that is perpendicular to a line = -10

Hence the correct answer is Option A