ANSWER
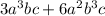
Step-by-step explanation
1. We want to expand the expression given:
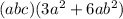
To do this, use the term in the first bracket to multiply each of the terms in the second bracket and then, simplify:
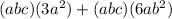
Now, simplify by multiplying the common terms in each product:
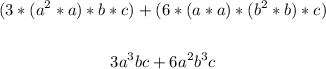
That is the answer.