We will determine the area of the shaded region as follows:
*First: We determine the area of the circle:
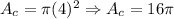
*Second: We determine the area of the hexagon:
**For this, we have that the internal angles of the sub triangles formed [in the hexagon] are:
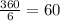
**Using this, we form two straight triangles and determine the value of the base of the triangle:
![6=b\sqrt[]{3}\Rightarrow b=\frac{6}{\sqrt[]{3}}](https://img.qammunity.org/2023/formulas/mathematics/college/p9u8ug8p2ko2slfjqzxtbgpqpo29heqdkb.png)
**Now, we determine the area of the hexagon:
![A_h=(1)/(2)(\frac{6}{\sqrt[]{3}})(6)\Rightarrow A_h=6\sqrt[]{3}](https://img.qammunity.org/2023/formulas/mathematics/college/ubevnyfi9pb9jj3k50w2pnpscukif00tyt.png)
*Finally: We subtract the area of the hexagon from the area of the circle:
![A_s=16\pi-6\sqrt[]{3}\Rightarrow A_s=39.9](https://img.qammunity.org/2023/formulas/mathematics/college/vj0bje29vrw8al43n2p3m14xxeoo0m12mx.png)
So, the shaded area is approximately 39.9 square feet.