Answer:
y = -2x + 9
Explanation:
slope intercept form : y = mx + b
where m = slope and b = y intercept
first let's find the slope
slope formula :
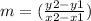
where the x and y values are derived from the given points
here we are given (2,5) and (6,-3)
(x1,y1) = (2,5) so x1 = 2 and y1 = 5
(x2,y2) = (6,-3) so x2 = 6 and y2 = -3
we now plug these values into the formula
recall formula
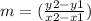
plug in x1 = 2, y1 = 5, x2 = 6 and y2 = -3
m = (-3 - 5) / ( 6 - 2 )
m = (-8)/(4)
m = -2
the slope is -2
now to find the y intercept we plug in the slope and the x and y value of a given point into slope intercept form and solve for b
y = mx + b
given point : (2,5) x = 2 , y = 5, m = -2
5 = -2(2) + b
5 = -4 + b
9 = b
so the equation would be y = -2x + 9