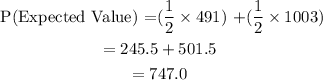Question

A person randomly selects one of six envelopes Each envelope contains a check that the person gets to keep. Determine the person's expectation if three envelopes contain a 491 check and three envelopes contain a 51003 checkThe expected value is $(Simplify your anwwer Type an integer or a decimal)

Answer 1

The probability formula is given by:

`\text{ P(E) =}\frac{\text{ N(Required outcome)}}{\text{ N(Total outcome)}}`

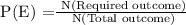
The person selects one of six envelopes.

There is a probability that the person selects an envelope that contains a $491 of 3 envelopes OR an envelope that contains a $1003 check of 3 envelopes

`\begin{gathered} \text{ P(select one containing \$491 check) =}(3)/(6)=(1)/(2) \\ \text{ P(select one containing \$1003 check) =}(3)/(6)=(1)/(2) \end{gathered}`

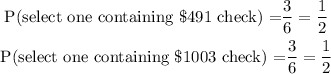
Then, the expected value is given by

`\begin{gathered} \text{ P(Expected Value) =(}(1)/(2)*491)\text{ +(}(1)/(2)*1003) \\ =245.5+501.5 \\ =747.0 \end{gathered}`