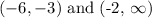Question

Determine the intervals on which the function is increasing, decreasing, and constant.List the interval(s) on which the function is increasing. [____]List the interval(s) on which the function is decreasing. [____]List the interval(s) on which the function is constant. [____]

Answer 1

The question asks to determine the intervals on which the function is increasing, decreasing, and constant. We can identify these intervals based on the slope of the function.

Step-by-step explanation:

The question asks to determine the intervals on which the function is increasing, decreasing, and constant. To do this, we need to analyze the slope of the function. If the slope is positive, the function is increasing, if it is negative, the function is decreasing, and if it is zero, the function is constant.

Based on the given information, we can determine the intervals as follows:

• Interval(s) on which the function is increasing: Part C, where the slope starts at zero and increases in magnitude until it becomes a positive constant.
• Interval(s) on which the function is decreasing: Part A, where the slope starts with a nonzero y-intercept and levels off at zero.
• Interval(s) on which the function is constant: Part B, where the slope starts at zero and decreases in magnitude until the curve levels off.

Answer 2

A function f is increasing on an interval when

`f^(\prime)(x)>0\text{ for all x in that interval}`

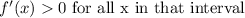
Also,

`\begin{gathered} f^(\prime)(x)>0\text{ for all x in that interval if the tangents to the curve at any point on the curve } \\ \text{ in that interval makes an acute angle with the positive x-axis} \end{gathered}`

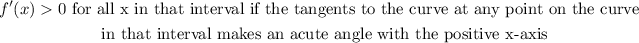
From the image,

the function has a maximum point at x = -8,

therefore

`\begin{gathered} f^(\prime)(x)>0\text{ for x < -8} \\ \text{ That is } \\ f^(\prime)(x)>0\text{ on (-}\infty,-8) \end{gathered}`

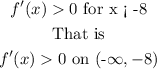
Also,

`\begin{gathered} f^(\prime)(x)>0,for \\ -30\text{ on (-3, -2)} \end{gathered}`

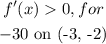
Hence, the function is increasing on the intervals

`(-\infty,-8)\text{ and (-3, -2)}`

b)

A function f is decreasing on an interval when

`f^(\prime)(x)<0\text{ for all x in that interval}`

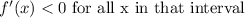
Also,

`\begin{gathered} f^(\prime)(x)<0\text{ for all x in that interval if the tangents to the curve at any point on the curve } \\ \text{in that interval makes an angle that is not acute with the positive x-axis} \end{gathered}`

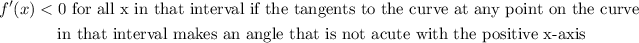
From the image,

the function has a maximum point at x = -8,

therefore

(c)

A function f is constant on an interval when,

`f^(\prime)(x)=0\text{ for all x in that interval}`

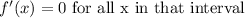
Also,

`f^(\prime)(x)=0\text{ for all x in that interval if the graph is parallel to the x-axis on that interval}`

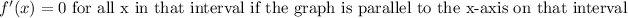
From the image, we can see that the graph is parallel to the x-axis on the intervals

`-6-2}`

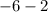
Hence, the function is constant on the intervals

`(-6,-3)\text{ and (-2, }\infty)`