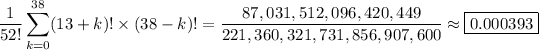Question

In a standard card deck, there are 52 different cards, which are divided into 4 suits (spades, diamonds, clubs, and hearts), with each suit containing 13 cards. What is the probability that in a randomly selected rearrangement of the card deck, the 3 of spades is after all the hearts

Answer 1

In a given permutation of 52 cards, if the 3 of spades is to follow all of the hearts, that means the 3 of spades must be at least the 14th card in the deck.

Consider some possible orderings of the deck:

• If the 3 of spades is the 14th card, then the deck looks like

[all 13 ♥] … 3 ♠ … [all other 38 cards]

There are 13! ways to arrange the 13 hearts at the beginning and 38! ways to arrange the tail of 38 cards. Hence there are 13! × 38! possible rearrangements of the deck where 3 ♠ is the 14th card.

• If 3 ♠ is the 15th card, then the deck looks like

[13 ♥ and 1 other] … 3 ♠ … [all other 37 cards]

and there would be 14! × 37! ways of arranging the cards in this order.

There are 39 possible positions for 3 ♠. Extrapolating, it follows that the total number of permutations of the deck in which all hearts occur before 3 ♠ is

`\displaystyle \sum_(k=0)^(38) (13+k)! * (38-k)!`

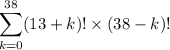
There are 52! total possible ways of rearranging the deck. Then the probability of rearranging the deck so that all hearts are drawn before 3 ♠ is

`\displaystyle \frac1{52!} \sum_(k=0)^(38) (13+k)! * (38-k)! = (87,031,512,096,420,449)/(221,360,321,731,856,907,600) \approx \boxed{0.000393}`